5.14天一杯最后一题
题面$$给定2023个数x_1,x_2,x_3,……,x_{2022},x_{2023} 满足\sum \limits_{i=1}^{2023}x_i^2=1$$$$求|x_1-x_2|+|x_2-x_3|+……+|x_{2022}-x_{2023}|+|x_{2023}-x_1|的最大值$$
思路看到这一题第一步想到的是代数变换你就已经输了,因为你再怎么变化都无法消去绝对值。所以这题最主要的是一眼看出本题的坑,当你想到换元时,你就已经做对一半了。
正解$$令y_i=x_i^2 \ , \ \therefore \sum \limits_{i=1}^{2023}y_i=1 \$$我们观察所求式子的形式,易得当原式取最大值时 $x_i, \ x_{i+1}$ 是不同正负的,即:$$x_ix_{i+1}<0, \ 1\leqslant i \leqslant 2022$$而 $x_1,x_{2023}$ 是同正负的,不妨设$x_1>0,x_{2023}>0$$$\therefore x_i=\sqrt{y_i} ...
AI行为大赏
Part 1 i have a dreamMartin Luther KingI have a dream that one day this nation will rise up and live out the true meaning of its creed: “We hold these truths to be self-evident, that all men are created equal.”
I have a dream that one day on the red hills of Georgia, the sons of former slaves and the sons of former slave owners will be able to sit down together at the table of brotherhood.
I have a dream that one day even the state of Mississippi, a state sweltering with the heat of injustice, s ...
Copyrighy by Wayne
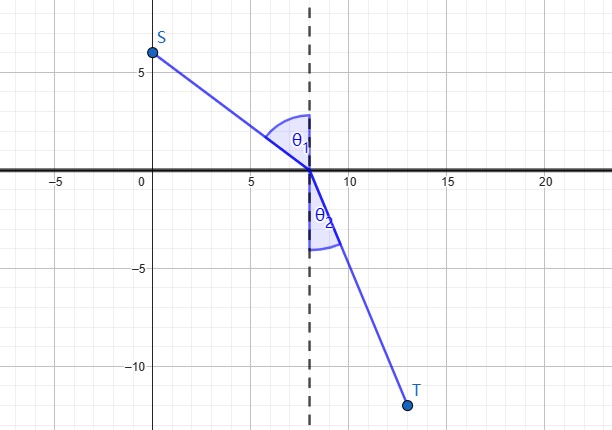
关于点线最值问题的微探究内容摘要: 在中学接触了一定量的最值问题后,发现了两类可以解析的最值类型,一是绝对值最值,即在数轴上的点和的最值。由此我们想到将其推广到更一般的形式,限于能力仅作部分推广。将最值问题从另一代数化的的角度去思考会发现别有一番洞天。 在中学接触了一定量的最值问题后,发现了两类可以解析的最值类型,一是绝对值最值,即在数轴上的点和的最值。由此我们想到将其推广到更一般的形式,限于能力仅作部分推广。将最值问题从另一代数化的的角度去思考会发现别有一番洞天。在中学接触了一定量的最值问题后,发现了两类可以解析的最值类型,一是绝对值最值,即在数轴上的点和的最值。由此我们想到将其推广到更一般的形式,限于能力仅作部分推广。将最值问题从另一代数化的的角度去思考会发现别有一番洞天。
关键词:最值,平面几何,解析几何,代数分析
一、费马点问题问题:在平面内的一个给定的三角形中,试求一点P使得该点到三角形各顶点的距离和最小。(费马点) 事实上,我们先对三角形进行分类:
$I.$对于最大角$\alpha = \angle A$ ,若$\alpha < 120^。$则取三角 ...
Musk人类之光
星舰首发失利就在4月17日,人类史上最大的一艘火箭——“星舰”首次发射,尽管以失败告终,再空中飞行一段时间后因为发动机熄火而导致其受力不均接体爆炸,但是再视频中我们依然可以听见指挥室最为响亮振耳的欢呼声,是的,没错一个美国人怀揣着一个世界梦正走向人类历史的转折之路,马斯克,无论如何都将载入史册,人类将永远铭记他这光辉的一天,未来历史上将会这样书写:埃隆马斯克,于2023年4月17日,率领公司Space-X发射了自土星五号以来最大的火箭,这已不是人类的跃进,更是未来火箭的一个新的起步……而我们便是历史的见证者。
埃隆·马斯克说起埃隆马斯克,更多的想到的是他是一个企业家,总领着最大的私营火箭公司Space-X与其其他公司如特斯拉等。作为世界首富,他却一点都不是一个首富的样子(我也没当过世界首富,我也不知道世界首富该是什么样子),哪会有一个人向民众夸下如此海口,“我们要去火星”上一个怎么说的人头盖骨已经都给人掀开了(肯尼迪“We choose to go to the moon”),他是一个敢于梦想的人,但如果仅此而已,她还只是一个梦想家。可他远不只是一个梦想家,还更是一个冒险家,开拓者以至 ...
2023平行四边形讲义
谁都不会想到这张破试卷有这么难,73分低出天际了,所以为了确定我是个渣,写了这篇题解,同时也为博客的数学公式的功能做一个小小的检测。下载typroa
这里提供一个typroa的下载地址,当然还是建议付费,支持开发者。
链接:https://pan.baidu.com/s/1PpMt21LcWAH4MJrNvaWxWQ
提取码:8jkp
试题
题解选择题第1题略(不会的自己旋转一分钟吧)
第2题分析:抓住题意 AD平行于BD 立马想到平行四边形的三大判定(双平行线;平行加相等;对角线互相平分),所以接下来我们只需关注以下条件能否转化为这三大形式由于$I.II.IV$太简单(秒出)所以这里只考虑剩下三种
$III(AD=BC).$这是一个十分典型的反例,平行+另一组对边相等并不能推出平行四边形,反例可构造等腰梯形。
$V(BO=DO).$这一种看到对角线条件,优先转化为第三判定定理。由对顶角+内错角可得$\Delta ABO\cong\Delta CDO$剩下的不用多说了。
$VI(\angle ADC =\angle CAB ). ...
Let's make pizza nicer again——by Donald Trump
My fellow Americans,
Let me tell you, nobody knows pizza like I do. And let me tell you, if you want to make the best pizza, you need to follow my advice.
First of all, you need to use plenty of cheese. And I mean plenty. Don’t be cheap with the cheese. And don’t overcook it either. You want that cheese to be nice and melted. That’s the key to a great pizza.
And when you cut the pizza, don’t just toss the slices on the plate. No, no, no. You need to stack those slices up tight. That way, the che ...
第一次搭博客有些紧张
这是我的第一个博客,向这个博客世界说一声你好,这不会是我唯一的博客,但是会是我走向自我的一个新的开始,怎么说呢,自从被一个名叫陈耕的小伙子骗来搭博客,至今还没完成,落下一堆事还没有完善,但是无论如何,但也算是一次大胆的尝试,个人觉得butterfly十分的膈应人,所以就先这样用着吧。
要说这个博客(Blog)干什么,没怎么想好,学习前人吧,fggirl会为我感到自豪的。他既然写题解,我也写题解,只不过得避讳着点几何题(画图真的很累人)。题解不是什么坏事,但是担心父母因此而数落自己:啊,你真么又在这里捯饬你的垃圾玩意儿,赶紧去写作业去,紧接着,就得停更一段时间。
不是每一个人都可以24h无断网的,所以这个博客更新也将会是离散的(奇妙的比喻)。(不会吧不会吧,真的会有人关注吗,但谁有会无聊地去看呢?)我写给自己,也算是作为一种慰藉吧:我在努力了,我在思考了,我在和自己对话。
生活处处会有烦心事,伟大的柯皓晟·廖子萱曾今在国文讲堂上发表过这样一篇演说,大致的内容可以概括:每一个人都需要一个吐露心声,吐诉自己的小小树洞。My Blog差不多也就充当这演一个角色罢了。或者说这是一面镜子,我一次一 ...